November’s IFT ZK Meeting (11/4) main topic will include a brief discussion on zk-SNARKs with small proof size. This year, multiple zk-SNARKs, Polymath (eprint 2024/916) and Pari (eprint 2024/1245.pdf), have been developed based on Groth16 that attempts to reduce the practical proof size.
Groth16
Groth16 gained popularity as it has the smallest proof among pairing-based zk-SNARKs. Specifically, a Groth16 proof consists of 3 group elements (2 from \mathbb{G}_1 and 1 from \mathbb{G}_2). It remains an open question whether a zk-SNARK can be constructed with a proof consists of only 2 group elements. Additionally, Groth16 proofs can be aggregated using SNARKpack (eprint 2021/529).
Groth16 lost some favor due to its reliance on circuit specific setups. That is, Groth16 requires a trusted setup (or ceremony) to construct the common reference string for each application. This restriction has helped in Plonk-based SNARKs from gaining popularity.
The 3 group elements make Groth16 an ideal proof for publishing on a blockchain. Due to this various projects (e.g., Nexus and RISCZero) use Groth16 as a compression layer.
Polymath
Polymath is a new zk-SNARK developed with an emphasis to minimize proof size with respect to the real storage space instead of the number of element group elements. In fact, in terms of theoretical size, Polymath has a larger proof than Groth16.
Polymath consists of 3 group elements (from \mathbb{G}_1) and a field element. This is one field element more than Groth16’s proofs consist of! In practice, elements from \mathbb{G}_2 require more storage space to represent than elements from \mathbb{G}_1. This observation is what Polymath builds off of.
Polymath uses a different circuit representation than Groth16. Instead of R1CS/QAP, Polymath uses the “lesser-known” squaring arithmetic program (SAP). A SAP consists of two gates: addition and squaring. We note that multiplication can be represented as in terms of these gates (with scalar multiplication): x\cdot y = 2^{-1}(x+y)^2 + 2^{-1}(x-y)^2. Hence, each multiplication gate in R1CS can be (naively) replaced with a minimal of 5 gates. Groth and Maller (eprint 2017/540.pdf) showed that a SAP constraint system has overhead at most two times that of R1CS.
Additionally, Polymath uses optimization techniques for Groth16 due to Lipmaa (eprint 2021/1700.pdf) which reduces the number of trapdoors from 5 to 2. As with Groth16, Polymath can use techniques from SNARKpack for aggregation.
Pari
Pari further improves on the concrete proof size of Groth16. Pari’s proofs consist of 2 group elements (from \mathbb{G}_1) and 2 field elements. Like Polymath, Pari uses SAP for circuit representation. The authors of Pari note that Pari could be adapted to use R1CS. This adaption would result in improved prover complexity but an increased concrete proof size (2 elements from \mathbb{G}_1 and 3 field elements).
Pari is not a modification of Groth16. Instead, Pari uses a new polynomial commitments that enforces equality of coefficients for a set of polynomials over different bases. This is used in a rowcheck argument
Comparison
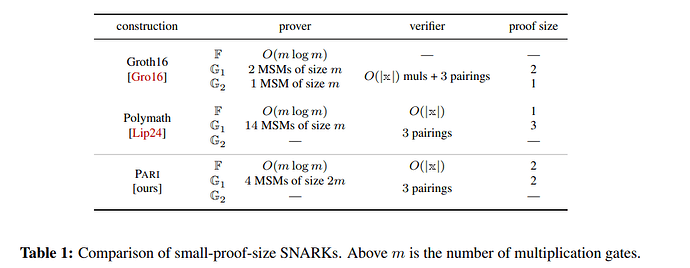
The following table comes from Pari (eprint 2024/1245):
Concretely, for the elliptic curve BLS12-381, a Groth16 proof uses1536 bits, a Polymath proof uses 1408 bits, and a Pari proof uses 1280 bits.
Conversation
Feel free to join in the conversation concerning these zk-SNARKs. Is the costs savings of a couple hundred bits per proof worth the hassle of potentially changing compression layers?