Some Mathematical Definitions
Coefficient form: If you have an array set such that a_0, a_1,..., a_k and if you assume that this data has a coefficient form then it defines a degree k polynomial f where f(x)=a_0+a_1x+a_2x^2+...+a_kx^k
Evaluation form: Assume that w is a primitive element of the field. If you have an array set such that a_0, a_1,..., a_k and if you assume that this data has an evaluation form then it defines the unique polynomial f where f(w^i)=a_i and the degree of f is less then k.
KZG Polynomial Commitment
Assume that g is the generator element of the group G, \tau is the secret element comes from trusted setup. Let,
f(x)=a_0+a_1x+a_2x^2+\cdots+a_dx^d=\sum_{i=0}^d a_ix^i is a polynomial of degree d. KZG polynomial commitment has 4 steps: setup, commitment of polynomial, proof evaluation and verification of the proof. The prover does the first three steps and the verifier does the last step, verification.
Setup
- Choose a generator g of a pairing-friendly elliptic curve group G.
- Select the maximum degree d of the polynomials to be committed to.
- Choose a secret parameter \tau and compute global parameters gp=(g,g^{\tau}, g^{\tau^2},\dots, g^{\tau^d}). Keep \tau secret and release the rest publicly.
Commitment of polynomial
-
Given f(x)=\sum_{i=0}^d a_ix^i, compute the commitment of f as follows:
com(f)=g^{f(\tau)}=(g)^{a_0}(g^{\tau})^{a_1}(g^{\tau^2})^{a_2}\cdots(g^{\tau^d})^{a_d}
Proof evaluation
- Given an evaluation f(u)=v, compute the proof \pi=g^{q(\tau)} where q(x)=\frac{f(x)-v}{x-u}
q(x) is a quotient polynomial and it exists if and only if f(u)=v.
Verification of the proof
- Given commitment C=com(f), evaluation f(u)=v, and proof \pi=g^{q(\tau)}, verify that
e(\frac{C}{g^v},g)=e(\pi,\frac{g^{\tau}}{g^u})
, where e is a non-trivial bilinear mapping.
In notation, this expression g^{a} refers to the elliptic curve point addition. i.e. g^a=[a]*g=g+g+\dots+g where g is the generator point of the group G.
We represent the evaluation of the commitment polynomial at the point u as follows:
eval(f,u)\to v,\pi
Verification function is also defined as follows:
verify(com(f),u,v,\pi)\to true/false
NomosDA Protocol Steps
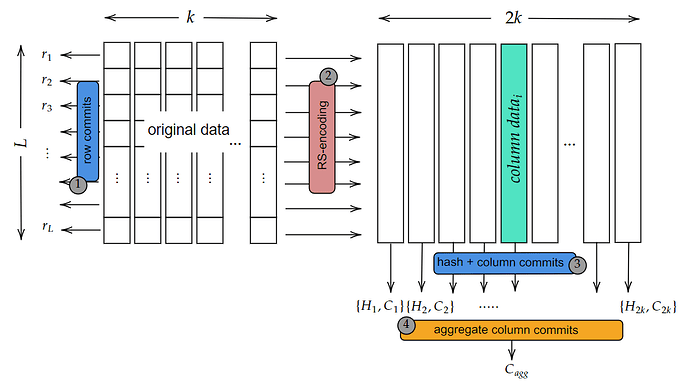
In NomosDA protocol, we will perform the RS-encoding and KZG process by dividing the data held in Zones into chunks. We will divide the block data into chunks in a way that each chunk represents a finite field element. The matrix representation of the data is as follows:
The length of each data_i^j value can be determined based on the finite field. Additionally, the row and column numbers used in the representation can be decided based on the size of the block data and the number of storage nodes. In NomosDA, we have k pieces which include \ell chunks each. (We will use BLS12-381 curve, thus each chunk value will be taken as 31 bytes to be a finite field element in implementation (31 bytes are chosen instead of 32 bytes because some 32 bytes will go out of scope of the bls12-381 modulus making it impossible to recover the data later))
The protocol for preparing data and commitments consists of four steps: calculating row commitments, expanding the original data using RS-encoding, calculating column commitments, and computing the aggregate column commitment value.
1-Row Commitments
Original data inputs are considered in the evaluation form, and unique polynomial values are calculated for each row.
Assume that for every row i, we have a unique polynomial f_i such that data_i^j=f_i(w^{j-1}) for i=1,...,\ell and j=1,...,k. Subsequently, KZG commitment values for these polynomials are computed as follows:
For each i=1,\dots,\ell,
- f_i=\text{Interpolate}(data_i^1,data_i^2,\dots,data_i^k) and compute r_i=com (f_i)
2-RS-Encoding
Using RS-encoding, the original data is expanded row-wise to obtain extended data. Due to the homomorphic property of KZG, the row commitment values calculated in the previous step are also valid for the row polynomial of the extended data.
- For redundancy, we can extend the blok data row-wise such that we evaluate data_i^j=f_i(w^{j-1}) these polynomials at the new points w^j where j=k+1,k+2,\dots,n. Now, we have extended data as follows;
We have a 1/2 expansion factor, hence we take n=2k. In this design, we plan to distribute each column to different storage nodes.
-
We also calculate the proof of each row chunk such that;
eval(f_i,w^{j-1})\to data_i^j, \pi_{data_i^j}
3-Hash and Commitment Values of Columns
In this step, we first calculate the commitment for the inputs of each column using KZG.
Assume j=1,\dots,2k
- Each column contains \ell chunks. Using Lagrange interpolation, we can calculate the unique polynomial defined by these chunks. Let’s denote this polynomial as \theta. The commitment values for each column are calculated as follows:
\theta_j=\text{Interpolate}(data_1^j,data_2^j,\dots,data_\ell^j)
C_j=com(\theta_j)
In this protocol, we use elliptic curve as a group, thus the entries of C_j 's are also elliptic curve points. Let’s represent the x-coordinate of C_j as C_j^x and the y -coordinate of C_j as C_j^y. If you have just C_j^x and one bit of C_j^y then you can construct C_j. Therefore, there is no need to use both coordinates of C_j. However, for the sake of simplicity in the representation, we use only the value C_j for now.
4-Aggregate Column Commitment
The position integrity of each column for all data can be provided by a new column commitments. Now, to link each column to one another, we will calculate a new commitment value.
-
We can consider each \{C_j\} as our new vector and assume they are in evaluation form. In this case, we can calculate a new polynomial \Phi and vector commitment value C_{agg} as follows:
\Phi=\text{Interpolate}(Hash(C_1), Hash(C_2),\dots,Hash(C_n))
C_{agg}=com(\Phi)
-
We also calculate the proof value \pi_{C_j} for each column.
We have to ensure that there is no opening for a new C_{n+1} commitment which means adding a new column to extended data. In this case, even if a new column is wanted to be added for the point n+1, the situation mentioned above will not be possible since it is computationally difficult to find data that corresponds to the committed hash value.
Verification Process
Zone sends the row commitments \{r_1,r_2,\dots,r_{\ell}\}, the proofs of row commitments \{\pi^j_{r_1},\pi^j_{r_2}, \dots,\pi^j_{r_\ell}\}, the column data \{data_1^j,data_2^j,\dots,data_\ell^j\}, column commitment C_j , C_{agg} and the proof of corrensponding column commitment \pi_{C_j} to the storage node node_j.
Storage Nodes
-
For the verification process, node_j, firstly checks the proofs of C_j and verifies the proofs. Zone calculates the eval value and sends it to node_j;
eval(\Phi,w^{j-1})\to C_j, \pi_{C_j}
-
Then, node_j calculates the commitment of column data and checks whether this value is equal to C_j or not.
\theta'_j=\text{Interpolate}(data_1^j,data_2^j,\dots,data_\ell^j)
C_j\stackrel{?}{=}com(\theta'_j)
-
After that, node_i firstly calculate the hash of the column commitment then verifies the proof:
verify(C_{agg}, Hash(C_j), \pi_{C_j})\to true/false
-
After that, for each r_i, the storage node verify the proof of every chunk against its corresponding row commitment as follows:
verify(r_i, data_i^j, \pi_{r_i}^j)\to true/false
-
If all verification succeed, then this proves that this column is encoded correctly.
This part was written in case of using VID scenario, but since the sampling protocol is now being applied, this part has become deprecated. It has been shared to give an idea of how the cryptographic process would work in the case of VID
In that case, node_j signs the certificate which consists of the hash value of C_{agg} and \{r_1,r_2,\dots,r_{\ell}\}.
-
Assume that the private key of node_j is sk_j. All storage nodes prove that they possess their private keys during the proof of possession stage initially. This stage is only done when storage nodes register in the system. It doesn’t need to be repeated with every signature. This process is needed to prevent the Rogue Key Attack.
-
Storage nodes that pass this check are added to the trusted list.
-
Every storage node j is generate the signature as follows:
\sigma_j=Sign(sk_j, hash(C_{agg}, r_1,r_2,\dots,r_{\ell}))
-
The signatures from storage nodes are verified by the dispersal, and valid signatures are collected in a pool. The size of the pool must be equal to or greater than the threshold value t. Then, these signatures are aggregated and the corresponding group public key is created as follows:
Aggregation:
- Given a set of signatures \sigma_1,\sigma_2,\dots,\sigma_t and corresponding public keys pk_1,pk_2,...,pk_t:
- Aggregate Signatures: \sigma_{agg}=\sigma_1+\sigma_2+\dots+\sigma_t
- Aggregate Public Keys: pk_{agg}=pk_1+pk_2+\dots+pk_t
Verification of Aggregated Signature:
- Given \sigma_{agg}, pk_{agg}, and the original message C_{agg}, r_1,r_2,\dots,r_{\ell}:
- Hash the message: h=H(C_{agg}, r_1,r_2,\dots,r_{\ell})
- Verify: e(pk_{agg},G)=e(\sigma_{agg},h)
- Given a set of signatures \sigma_1,\sigma_2,\dots,\sigma_t and corresponding public keys pk_1,pk_2,...,pk_t:
When the signatures are collected from each storage node, if it exceeds the threshold value, this will give us the proof that the data is encoded correctly and the integrity of the original data has been ensured.
Light Nodes
-
Light nodes, firstly choose a random t\in{1,\dots,2k} value and t'\in{1,\dots,\ell}.
t determines the column number, and t' determines the row number. That is, these values are selected for checking the chunk located at the t-th column and t’-th row. Light node wants to opening of C_t and r_{t'}.
-
Hence, node_t calculates the eval value for the column commitment and sends it to the light node;
eval(\Phi,w^{t-1})\to C_t, \pi_{C_t}
verify(C_{agg},C_r, \pi_{C_r})\to true/false
-
Also, light nodes get the r_{t'} value and the corresponding proof value from the chain. Light nodes verifies the row commitment as follows:
verify(r_{t'}, data_{t'}^t, \pi_{r_{t'}}^t)\to true/false
-
If this proof holds, then light nodes wants to opening of the column commitment. node_r calculates the eval value and also sends it to the light nodes:
eval(\theta_t,w^{t'-1})\to data_{t'}^{t},\pi_{data_{t'}^{t}}
verify(C_t, data_{t'}^t, \pi_{data_{t'}^t})\to true/false
If this holds, then this proves that the chunk data_{t'}^t is encoded correctly. If the light node queries multiple chunks of the same column, the batch commitment scheme helps have a single proof for all the sampled points.
Design Principles
In this section, we will discuss the design philosophy of NomosDA. Firstly, the reason for expanding the original data row-wise is to ensure data availability by sending a column to each storage node and obtaining a sufficient number of responses from different storage nodes for sampling. In our design, three different commitment values are calculated. Row commitment values are calculated to verify the accuracy of the RS-encoding process, column commitment values are computed for checking the ordering within a column and ensuring chunk integrity, while the aggregate column commitment value is calculated to ensure column ordering control.
We also show how the equivalence between the data held in Zone and the data sent to the nodes is ensured in the protocol. The original data was initially expanded with RS. Then, the commitment values for each column were calculated using KZG. These calculated commitments guarantee the integrity of the data within each column. Subsequently, since the column commitments are linked with a separate commitment, having any k of these columns will be sufficient to reconstruct the original data. This way, by applying sampling ( or aggregating the signatures from the storage nodes in case of VID scenario) without downloading the entire data, the equivalence can be proven.
In this design, there are three different commitment calculations. The row commitment values are defined to ensure the RS encoding control of the data sent to storage nodes and the order binding of the relevant chunk value through the row commitment. The column commitment values guarantee the position binding in terms of rows in the data encoded by the Zone without the need for super nodes. Without this calculation, the Zone could change the row order of the data it holds enabling attacks on DAS. With these two commitment values, the positions of the original data on the x and y axes are bound.
The final calculated C_{\text{agg}} commitment value guarantees the order of the column commitments. Due to bandwidth issues, instead of sending each column commitment value to all storage nodes, a single aggregate commitment value is calculated and this value is sent to the storage nodes. This also prevents adding new columns to the original data. Additionally, storage nodes will sign the C_{\text{agg}} value, thereby fixing the column order. (Since the storage nodes already had the row commitments, they were handling the row part by signing the hash value of these row commitments.)
ps: As a new user, I was only able to include one diagram. The other diagrams can be found on the Nomos notion page