Plausible deniability in Distributed Storage Networks

Vac
1

Codex, within its research roadmap, aims at providing plausible deniability to storing nodes in decentalized storage networks. Their requirements for a prospective solution are:

  1. Interaction between data “owner” and data “user” must be minimal.
  2. Data must be encrypted but universally accessible. This means that anyone should be able to obtain it.
  3. Only symmetric encryption should be directly used on data for efficiency reasons.
  4. The storing node must be oblivious with regards to the data it stores.
  5. The storing nodes cannot get access to the encryption key.
  6. MPC techniques, such as secret sharing or key distribution, must be avoided.

The Vac ACZ Unit is providing support by working on a solution. Among the possible solutions to this problems, we have the following:

  • Basic design

    We could look for techniques to hide the encryption key in the metadata. This approach can be straightforward in terms of implementation and efficiency, but does not provide plausible deniability and is prone to suffer a range of attacks.

  • Proxy re-encryption (PRE)

    PRE, see Núñez et al. for a reference, allows a 3rd party, a proxy, to transform data encrypted by Alice so that it can be decrypted by Bob using his own secret key, and with the proxy learning nothing about the data sent by Alice. PRE involves the usual Key generation, Encryption and Decryption schemes, and also an additional couple called where all the magic happens: Re-encryption key generator and a Re-encryption scheme. The re-encryption key generator will take Alice’s public and secret key, together with Bob’s public key, and will produce a re-encryption key, which will be used in the re-encryption key generator to produce a fresh re-encryped message. The latter data will be accessible to Bob.

    The syntax of a PRE scheme follows:

    1. KeyGen(k) → (PK, SK): On input security parameter k, this algorithm outputs a pair of public and secret keys (PK, SK).
    2. ReKeyGen(PK_A, SK_A, PK_B) → RK_A→B: On input the pair of public and secret keys (PK_A, SK_A) for user A and the public key PK_B for user B, this algorithm outputs a re-encryption key RK_A→B.
    3. Enc(PK_A, M) → CT: On input the public key PK_A and a message M, this algorithm outputs a ciphertext CT_A.
    4. ReEnc(RK_A→B, CT) → CT_B or ⊥: On input a re-encryption key RK_A→B and a ciphertext CT_A, this algorithm outputs a second ciphertext CT_B or the error symbol ⊥ indicating a re-encryption failure.
    5. Dec(SK_B, CT_B) → M: On input the secret key SK_B and a ciphertext CT_B, this algorithm outputs a message M or the error symbol ⊥ indicating a decryption failure.

    Taxonomy of PRE schemes

    1. Identity-based: public keys are replaced by identities between sender and receiver.
    2. Unidirectional: decryption rights are delegated only from delegator to delegatee, and
      not in the other direction.
    3. Bidirectional: in this context it is possible to compute re-encryption keys RK_A→B and RK_B→A. Not necessarily a bad property; bidirectional schemes would be appropriate for scenarios where the trust relationship between delegators and delegatees is symmetric.
    4. Key-private, or anonymous: impose an extra level of confidentiality by requiring pseudo-random proxy keys that leak no information on the identity of the delegators and delegatees
    5. Universal: they enable a proxy to convert a ciphertext under a delegator public key of any existing PKE scheme into another ciphertext under a delegatee public key of any existing PKE scheme (possibly different from the delegator one). This primitive is in a very early, theoretical stage.
    6. Symmetric: proxy re-encryption schemes suitable for symmetric encryption, rather than asymmetric schemes.

    PRE offers plausible deniability, since the storing node is responsible for re-encrypting akready encrypted data. Nevertheless, PRE requires interaction between user and owner due to the fact re-encryption keys require information from both sides. Also, there is a range of attacks motivated by malicious storing nodes. Furthermore, the storing node could set relations between users by analyzing the traffic of interactions.

    The usual approach for the use of PRE, and ABE as we will see later, is the lockbox technique a classic way-to-go where we do not use PRE on the whole data, but on the symmetric key used on that data.

  • Attribute-based encryption (ABE)

    Attribute-based encryption, see Herranz’s reference, allows data to be encrypted based on a set of attributes, rather than just a specific person’s key. It’s a more flexible approach to controlling access to encrypted data. This approach allows avoiding any interaction between users since the decryption ability is derived from the attribute universe. To make data universally accessible, we may consider a small attribute universe.

    In ABE we have the following syntax:

    1. Setup(k) → (MK, EK): This algorithm initializes the scheme and randomly creates and returns a master key MK and the public parameters EK. The master key is kept secret by the key authority, whereas the public parameters are made public and used to encrypt data.
    2. Encrypt(M, T, EK) → CT: This algorithm encrypts a message M associated with the access policy T, by means of the public parameters EK. It returns the encrypted message CT, which embeds the given access policy.
    3. KeyGen(A, MK) → DK: This algorithm creates a new decryption key associated with the attribute set A, by means of the master key MK. It returns the decryption key DK, which embeds the given attribute set.
    4. Decrypt(CT, DK) → M or ⊥: This algorithm decrypts a ciphertext CT with the decryption key DK. It returns the original message M if and only if the access policy T evaluates to true on the attribute set A embedded in the decryption key DK; otherwise, it returns the symbol ⊥ indicating a decryption failure.

    We observe that:

    • Encryption is done by the owner with a private set T of access policies (set by owner).
    • The decryption key does not rely on the encryption key in any way.

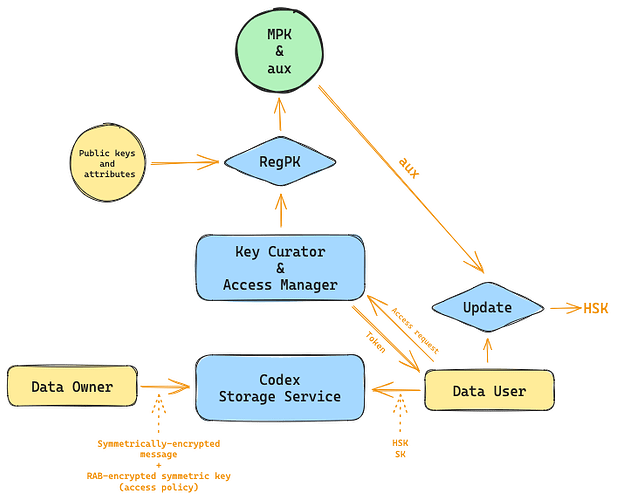
    The main problem with ABE is the key escrow problem, due to the fact that ABE requires an authority in charge of generating decryption keys, a Key Master Generator. Nevertheless, this can be avoided with a recent approach called [Registered ABE] (RABE), see Hohenberger’s paper for a reference, where the key master generator is replaced with a “key curator” which is public and auditable and does not hold any authority on the master keys, it only registers and updates public keys from other users and brings helper decryption keys.

    A RABE scheme is composed of the following algorithms:

    1. Setup(k, |U|) → crs: On input the security parameter k and the size of the attribute universe U, the setup algorithm outputs a common reference string crs.

    2. KeyGen(crs, aux) → (PK, SK): On input the common reference string crs, and a (possibly empty) state aux, the key-generation algorithm outputs a public key PK and a secret key SK.

    3. RegPK(crs, aux, PK, S) → (MPK, aux′): On input the common reference string crs, a (possibly empty) state aux, a public key PK, and a set of attributes S ⊆ U, the registration algorithm deterministically outputs the master public key MPK and an updated state aux′.

      Action 3 is performed by the key curator

    4. Encrypt(MPK, P, M) → CT: On input the master public key MPK, an access policy P, and a message M, the encryption algorithm outputs a ciphertext CT.

    5. Update(crs, aux, PK) → HSK: On input the common reference string crs, a state aux, and a public key PK, the update algorithm deterministically outputs a helper decryption key HSK.

      Action 5 is performed by the key curator

    6. Decrypt(MPK, SK, HSK, CT) → M or {⊥, GetUpdate}: On input the master public key MPK, a secret key SK, a helper decryption key HSK, and a ciphertext CT, the decryption algorithm either outputs a message M, a special symbol ⊥ to indicate a decryption failure, or a special flag GetUpdate that indicates an updated helper decryption key is needed to decrypt.

    Below follows a possible architecture, which follows the lockbox approach:

Figure_2
Figure_2708×573 62.7 KB

  • Witness encryption (WE)

    ABE and RABE are somehow similar to witness encryption. In a witness encryption scheme, we can encrypt a message in such a way that it can only be decrypted if a specific piece of information, called a “witness”, is provided. This witness is a solution to a complex problem.

    • There is a relationship R associated with the complex problem. If an instance x is part of a certain set L, then there is some witness w that confirms this, meaning (x,w) belongs to R. If x is not in L, then no such witness exists.
    • The encryption scheme ensures that if the witness is made public during decryption, the message is also revealed publicly.

    Witness encryption ensures that the encrypted message can only be accessed if someone has the correct solution to a complex problem, thereby securing the message against unauthorized access.

    In this setting, we has the construction Cassiopeia, by Saereesitthipitak et al., which is a smart-contract based construction for witness encryption. Nevertheless, this scheme relies in several primitives required to be avoided (secret sharing and threshold schemes) together with a trusted and fixed committee in charge sharing the encrypted secrets of users. These secrets are shared among the members of the committee, which are are required to use a secret sharing scheme to reconstruct them in case of being presented with a valid witness.

Let’s compare both approaches with regards to the requirements set by Codex:

PRE ABE/RABE WE Basic Design
Minimal interaction between users :x: :white_check_mark: :white_check_mark: :white_check_mark:
Universally accessible encryption :x: :white_check_mark: :white_check_mark: :white_check_mark:
Oblivious storing node :white_check_mark: :white_check_mark: :white_check_mark: :x:
Encryption key not accessible :white_check_mark: :white_check_mark: :white_check_mark: :x:
MPC avoided :white_check_mark: :white_check_mark: :x: (Cassiopeia) :white_check_mark:
Symmetric-encryption based :white_check_mark: :white_check_mark: :white_check_mark: :white_check_mark:

We use symmetric encryption as part of a lockbox approach.

Apparently registered attribute based encryption looks like the best approach to the problem of plausible deniability, and could be a quite innovative way to solve the problem. The main drawback is that RABE has high requirements and offers poor efficiency and results when it comes to its applicability, although research, such as Garg et al., to overcome these issues is on the way.

Discussion

The main objective of this post is to open a discussion on the approaches to a solution to the plausible deniability problem, according to Codex’s requirements; either revolving around the above possible solutions or introducing alternative approaches which were not considered.

References

  1. Garg, Rachit, et al. “Reducing the CRS Size in Registered ABE Systems.” Annual International Cryptology Conference . Cham: Springer Nature Switzerland, 2024.

  2. Saereesitthipitak, Schwinn, and Dionysis Zindros. “Cassiopeia: Practical On-Chain Witness Encryption.” International Conference on Financial Cryptography and Data Security . Cham: Springer Nature Switzerland, 2023.

  3. Nuñez, David, Isaac Agudo, and Javier Lopez. “Proxy re-encryption: Analysis of constructions and its application to secure access delegation.” Journal of Network and Computer Applications 87 (2017): 193-209.

  4. Herranz, Javier. “Attribute‐based encryption implies identity‐based encryption.” IET information security 11.6 (2017): 332-337.

  5. Hohenberger, Susan, et al. “Registered attribute-based encryption.” Annual International Conference on the Theory and Applications of Cryptographic Techniques . Cham: Springer Nature Switzerland, 2023.

2 Likes
2

This is great work @Ramses! So glad to see it being shared here as well.

I really enjoyed reading through the options and how they fit within the requirements given.

Were the requirements discussed, justified, or questioned at all? Do you see any meaningful reason to relax any of them?

edit: oxford comma

3

How do you define owner and user in this context?

What is the reasoning behind this requirement?

4

I am happy to know you enjoyed it!

The requirements were discussed with the Codex team and all of them revolved around keeping complexity and the surface of attacks as small as possible. On the other hand we had some discussions within Vac concerning the possible techniques that could be applied.

The main reasons leading to relaxing requirements would be complexity and efficiency. For example, the best approach would be registered ABE, but this solution although it fulfills all the requirements, is in a pretty early stage in terms of research and does not offer the best results in terms of efficiency (although it is pretty good at it). Relaxing registered ABE would lead to an approach similar to Cassiopeia (WE), if one bears with MPC.

5

What we mean when we say owner is the user uploading data. A user is whoever wants to get access to that data.

The main reasons to try to avoid MPC is to keep interactions within the protocol at a minimum. This would result in a simpler solution, with a smaller range of attacks.