Integration of Efficient Proof of Equivalence

[kd14]

Objective

Zones (rollups) use the Base Layer for Data Availability. They send data as blobs. To the Base Layer, DA clients prove that the data is correctly encoded.

However, the data that is sent to DA is in no way bound to anything. Without any cryptographic proof, the data it’s just that: arbitrary data. The objective is to prove that the data posted by the Zone to the Base Layer is the same one required for the state reconstruction: the witness of the ZK proof of state transition.

Problem Statement

We need to prove that B (the data in the blob) is the same as the data used for the state diff within the ZK STF (state transition function) proof:

B = d_0, ..., d_{n-1}

Generally we would want to do this directly with two separate commitments, and check their equality. Otherwise we would be defeating the purpose of using DA in first place, as the checker would need to have the data on both sides of the equation available to perform the check. The test then becomes C = C^\prime with:

• C the KZG commitment to P_B
• C^\prime the KZG commitment to P_{d_0,…,d_{n-1}}

The equality of the commitments guarantees with sufficient security the equality of the two polynomials: P_B = P_{d_0,…,d_{n-1}}, ie the two encodings are equivalent, thus B = d_0, ..., d_{n-1} holds true.

However, we face an important challenge: since the C^\prime commitment is computed within the ZK environment, the calculation needs to be ZK-friendly to be practical. A polynomial commitment like KZG has two problems:

• It is not ZK friendly.
• It is enforced onto the Zone, with a loss of sovereignty and an increase in complexity.

The protocol described here works around this limitation and allows proving the data equivalence without requiring the computation of a polynomial commitment within a ZK snark, allowing the use of much more efficient commitments.

Protocol

The following protocol is an adaptation of the method used by Starknet.

Definitions:

• State diff data d_0, ..., d_{n-1}. This is the data used by the Zone directly to perform the state transition. This is the data used for state reconstruction, and what we need to make available for security to hold.
• Blob data B. This is the data actually sent to the Base Layer.
• C is the KZG commitment of d_0,...,d_{n-1}. The CL has access to it, as it has been sent to every node in the BL/CL.

Protocol:

1. Data encodings, performed by the Zone
   1. Encode the state diff in coefficient form:
      P_\text{diff}(x) = \sum_{i=0}^{n-1}d_ix^i
      Note that this is the data encoded directly as employed by the ZK prover.
   2. Encode the state diff for DA:
      P_B = \widetilde{d_0},...,\widetilde{d_{n-1}} where \widetilde{d_i}=P_\text{diff}(\omega_i), where \omega_i,...,\omega_{4096} are the first roots of unity of order 4096 over the BLS12-381 field.
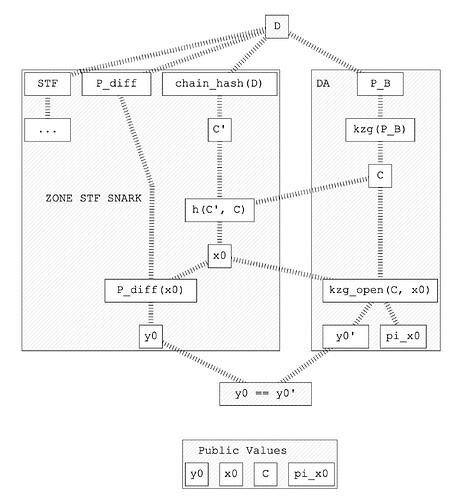
2. Zone STF Prover

   1. Inputs: \{P_\text{diff}, C\}
      P_\text{diff} is a witness, and C is a public input
      Explanation: we pass the encoding of the data as it will be used by the STF prover. We also pass the KZG commitment sent to the Base Layer (which is a random string from the perspective of the Zone), allowing the prover to use it for the point for Fiat-Shamir.

   2. Proves:

      1. Correct execution of the Zone STF using P_\text{diff} (ie the transactions)
      2. Correct computation of ZK-friendly C', a chain-hash of d_0,...,d_{n-1}
      3. x_0 = h(C,C') This is a “random” point (Fiat-Shamir heuristic)

      Explanation: what matters here is that C' is binding, but other than that is only used for generating the provable randomness required for the generation of x_0, later on used to prove the equality.

   3. Output: \{C, x_0, y_0\}, where y_0 = P_\text{diff}(x_0)

3. Verification
   1. Inputs: \{C, x_0, y_0\, \pi_{x_0}\}, where \pi_{x_0} is a proof of the opening of C at x_0, and all the inputs are public.
   2. Verifies:
      1. The statement P_B(x_0) = y_0, therefore P_B(x_0) = P_\text{diff}(x_0).
      2. This verifies w.h.p. that P_B = P_\text{diff}

Note that we need to have the equivalent to the point evaluation precompile that Ethereum has, to allow the verification of the point openings in the CL

The key ideas are:

• We don’t need to prove the equality of the commitments in ZK, nor generate the commitment to be proven equal within the ZK. Rather, we can just prove that:
  • The polynomial directly encoding the state diff within the ZK is y_0 at the provably randomly selected point x_0.
  • The polynomial encoding the state diff in the DA form is also y_0 at that x_0.
  • x_0 is verifiably random and cannot be biased by the prover.
• The internal ZK-friendly commitment is just used to generate “randomness” to pick a point to prove the equality of the two encodings. Thus it needs to be binding to the data, but it can be any type of commitment that fulfills that requirement without the need to be polynomial.

Implementation

The pseudocode for implementing the PoE protocol, using Risc0 and integrating it into the CL side, was initially prepared as follows.

# Version 1: PoE is within the STF
# Pseudocode for Proof of Equivalence (PoE) Protocol

# Definitions
# P_diff: Polynomial encoding of state diff data used by the Zone STF
# P_B: Polynomial encoding of blob data sent to the Base Layer (DA)
# C: KZG commitment of P_diff, available to the Base Layer and CL
# C': ZK-friendly commitment of state diff data used within the ZK proof
# x0: Random point generated using Fiat-Shamir heuristic
# y0: Evaluation of P_diff at x0
# y0': Evaluation of P_B at x0
# pi_x0: Proof of the opening of C at x0

# Step 1: Zone encodes data
def encode_data(state_diff_data):
    # Encode state diff in coefficient form
    P_diff = polynomial(state_diff_data)

    # Encode state diff for DA
    P_B = [P_diff(omega_i) for omega_i in first_roots_of_unity(4096)]

    return P_diff, P_B

# Step 2: Zone STF Prover generates proof
def zone_stf_prover(P_diff, C):
    # Compute ZK-friendly commitment C'
    C_prime = chain_hash(P_diff)

    # Generate random point x0 using Fiat-Shamir heuristic
    x0 = hash_function(C_prime, C)

    # Evaluate P_diff at x0
    y0 = P_diff.evaluate(x0)

    # Output values for verification
    return C, x0, y0

# Step 3: Verification by DA clients
def verify_proof(C, x0, y0, pi_x0):
    # Open the KZG commitment at x0 to get y0'
    y0_prime = kzg_open(C, x0)

    # Verify that the evaluations are equal
    if y0 == y0_prime:
        return True  # The data is equivalent
    else:
        return False  # The data is not equivalent

# Main Protocol Execution
def main():
    # Step 1: Zone encodes state diff data
    P_diff, P_B = encode_data(state_diff_data)

    # Step 2: Zone STF Prover generates proof
    C, x0, y0 = zone_stf_prover(P_diff, C)

    # Step 3: DA clients verify proof
    is_valid = verify_proof(C, x0, y0, pi_x0)

    if is_valid:
        print("Proof of Equivalence is valid. Data is equivalent.")
    else:
        print("Proof of Equivalence is invalid. Data is not equivalent.")

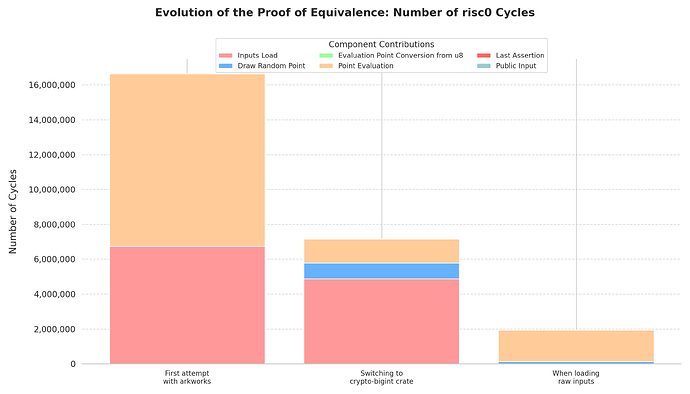
Subsequently, work began on a PoC implementation. After the first implementation attempts, it was understood that performing the polynomial evaluation within the STF could impose a significant load. The implementations and improvements made at this stage can be seen below:

Progression

Cycles per function	First attempt with arkworks	Switching to crypto-bigint crate	When loading raw inputs
inputs load	6,739,091	4,878,576	4,879
draw random point	1,106	903,158	120,701
evaluation point conversion from u8	6,679	17	17
point evaluation	9,879,111	1,365,391	1,811,826
last assertion	6,914	79	79
public input	10,001	5,939	9,945
total	16,645,963	7,156,776	1,950,977

• We started with a simple implementation using arkworks for representing elements of the BLS12-381 scalar field. Using arkworks to evaluate, build polynomial and scalar structure wasn’t good as the number of risc0 cycles were around 500k for polynomials with 32 coefficients. We used Horner’s evaluation method for performance.
• Moving from arkworks to crypto-bigint, an optimized crate of big unsigned integer for risc0, we reduced the number of cycles to 7.1M for 2048 coefficients.
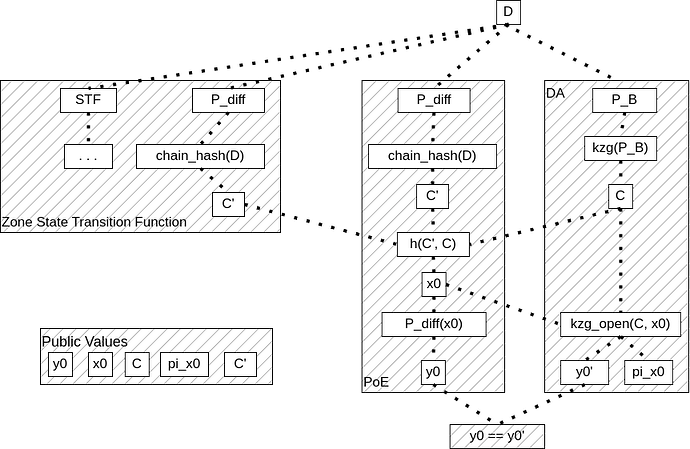
• The larger number of cycles was coming from input reading and serialization into structure. Instead of using the classical env::read() of risc0 that provenly construct the rust structure, we provided inputs as bytes using env::read_slice() , that was then converted manually when needed into scalar elements. This step reduced the number of cycles to 1.95M for 2048 coefficients.
• For now, proof of equivalence was supposedly included in the STF so the STF can directly used the proven data. Since the PoE is 2M cycles, it can also be interesting to externalize this PoE, hard coding it in a Circom circuit. The diagram of the protocol would then become:

In Circom:

constraints	SnarkJS proving time	Tachyon CPU proving time	proving key size	witness generation time
78,346	8.540 s	3.059 s	115.7 MB	113 ms

Important details

It’s important to note that, to prove that two different commitment schemes commit to the same polynomials, they must be the same polynomials in a mathematical sense. This means that, in addition to having the same coefficients, they must also reside in the same field.
So when the evaluation is performed on the hash of the commitment, the result are the same (because the operations are done under the same modulus). This can increase the complexity of the proof in the case where the STF operates under a different modulus than the BLS scalar field (chosen for the data availability layer) because it needs to emulate this modulo in a different modulo. (emulating \mathbb{F}_p operations in \mathbb{F}_r).

That’s explaining why it’s so costly in risc0, because we need to emulate BLS scalar field operations using the crypto-bigint library (which is already optimized, see the first cycles gain comparing crypto-bigint and ark-ff use).

Integration

The PoE can either be the responsibility of the zone but can also be verified by the CL through the zone note covenants (previously death/birth constraints). In this case, the proof produce the evaluation on a random point behind a hash commitment. The CL need to verify this proof, that the STF use the data behind the produced hash AND a KZG proof of the data availability layer proving the evaluation of the data on the same random point leads to the same evaluation.