Hash Functions - Reinforced Concrete, Poseidon and Monolith

1

This forum thread is for discussion leading up to and following November’s IFT ZK Call.

SHA-2 and Keccak are often the first hash functions that come to one’s mind. However, in recent years, new hash functions have gained popularity. Hash functions such as Reinforced Concrete and Poseidon (and its successor Poseidon2) were designed with arithmetic circuits in mind.

Traditional hash functions were designed with two main priorities: security and evaluation efficiency. Unfortunately, traditional hash functions become a bottleneck for incremental verification due to the number of constraints that are required. Reinforced Concrete and Poseidon were designed with this in mind. Such hash functions are called SNARK-friendly.

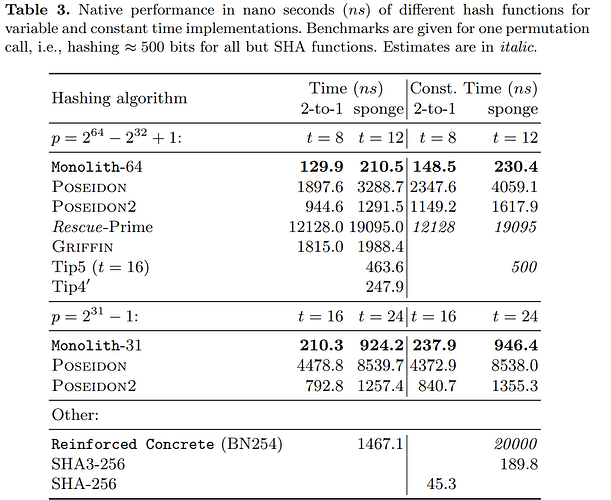
Reinforced Concrete uses Poseidon’s design strategy. Specifically, Reinforced Concrete and Poseidon use two different rounds to protect them from statisical attacks and algebraic attacks. Reinforced Concrete is 5 times faster than Poseidon. Table 2 in Reinforced Concrete’s paper (eprint 2021/1038) provides a comparison benchmark between Reinforced Concrete and a variety of hash functions (including Poseidon).

How does Reinforced Concrete achieve this? By use of lookup tables and by replacing field multiplication with modular reductions.

Monolith offers improved performance over Poseidon and Reinforced Concrete. Monolith uses lookup arguments with simple CPU instructions. This allows for Monolith to be parallelizable and runs in constant-time. Monolith is protected against side-channel attacks due to its ability to be evaluated in constant-time.

In the paper for Monolith (eprint 2023/1025):

monolith_table
monolith_table1055×862 125 KB

The performance given for Reinforced Concrete in Monolith’s table is only an estimate. This is due to the implementation used for Reinforced Concrete to be unoptimized. Based on Reinforced Concrete’s paper claim, I would expect that Reinforced Concrete would evaluate sponge for p = 2^{64}-2^{32}+1 in \approx 660 ns. It is unclear why Monolith’s team did not test Reinforced Concrete in this case (and p = 2^{31}-1).

Reinforced Concrete does not appear to have gained traction in the community that Poseidon/Poseidon2 has. Additionally, Monolith appears to be a promising hash function which may seem wider adoption.

2

So some of the recent candidates for a good arithmetic hash functions are:

  • Rescue Prime (any prime field)
  • Poseidon (any prime field)
  • Poseidon2 (any prime field)
  • Reinforced Concrete (any prime field, needs lookups)
  • Tip5, Tip4 (only the Goldilocks field, needs lookups)
  • Monolith (only specific field: Goldilocks or Mersenne31 fields, needs lookups)
  • Skyscraper (any prime field, needs lookups)

Apart from Rescue Prime and Tip5/4, all of these came out from the same group of
people. The order is probably not too far from the historical order.

Some comments:

  • Rescue Prime is a genius idea of having very efficient in-circuit implementation,
    by using inverse powers (like x -> x^(-5)) for sboxes. However, this also makes
    it very slow on CPU. So this can be a good choice where the proof cost is
    the most important one.

  • Poseidon and Poseidon2 are a good baseline hash function. They use linear
    diffusion and small power (like x -> x^5) for nonlinearity

  • Reinforced Concrete introduces table-based sbox-es into the same approach,
    which essetially kills algebraic attacks, so you need much less rounds
    (previously the number of rounds were mostly determined by estimates for
    algebraic attacks). However, a general problem with mixing table-based
    sbox-es with prime fields is that the resulting function is not a permutation
    of [0..p-1]. The way RC solves this is very convoluted, hard to implement,
    and inefficient.

  • Monolith solves this problem by using specific primes: In case of Goldilocks,
    p-1 = 0xFFFFFFFF00000000. If you subdivide into bytes, apply an sbox to
    each byte, for which 0x00 and 0xFF are fixed points, then you automatically
    get a permutation of [0..p-1]. It also uses squareings instead of higher powers for
    nonlinearity. This is very efficient on CPU, but only works for very
    specific primes (in particular, not compatible with elliptic curve based
    proof systems)

  • Tip5 is quite similar to Monolith, but uses a bit different design (also
    came out a bit earlier I think), and mixed table-based and small-power
    sbox-es. Apparently Monolith is about 2x faster. There also some variations
    like Tip4 and Tip4’

  • Skyscraper fixes the problem of Monolith requiring particular fields by
    noticing that with a Feistel-network construction, you can always construct
    a permutation out of a non-permutation. Apparently this is similarly fast
    as Monolith.

Codex started with Poseidon2 on the BN254 curve’s scalar field (because we
started with Groth16, which is elliptic curve based and has no lookup tables,
so we didn’t really had any other choice). For Codex, CPU performance is
critical, so we plan to switch to Monolith soon. On the long-term we even
hope to keep the option of using SHA256 open, if we can figure out an
efficient enough proof system for that.

My choices would be:

  • if only the in-circuit performance (proof time) matters, CPU performance doesn’t, the use Rescue Prime
  • if only CPU performance matters, proof time doesn’t, use SHA256
  • otherwise, if you don’t have lookup tables, use Poseidon2
  • if have lookup tables and you can use either Goldilocks or Mersenne31 field, use Monolith
  • if you need other (for example large) fields, but still have lookup tables, use Skyscraper